Loi de Dalton
![]()
 Le
plongeur sportif respire de l'air comprimé.
Le
plongeur sportif respire de l'air comprimé.
L'air n'est pas un gaz unique mais un mélange de gaz composé de :
| - Azote (N2) --> 79.03% | |
| - Oxygène (O2) --> 20.93% | |
| - Gaz carbonique (CO2) --> 0.03% | |
| Plus quelques traces de gaz rares |
- Pour la commodité des calculs, nous considérons qu'il y a 20% d'oxygène et 80% d'azote dans l'air.
- L'oxygène est le gaz vital, c'est le comburant nécessaire au métabolisme cellulaire.
- L'azote ne set à rien, si ce n'est le diluant de l'oxygène, il est neutre.
DALTON a précisé quelques phénomènes observés tous les jours tels que :
- La présence d'un gaz nocif dans l'air que l'on respire peut être soit inoffensif, soit provoquer des malaises, ou même être fatale. Tout dépend de la quantité de gaz qui s'y trouve. Le fait qu'il soit mélangé à un autre gaz n'empêche pas ses effets.
=> Un gaz exerce sa propre action comme si il était seul
- Lorsque vous laissez échapper une petite quantité de gaz de votre gazinière, l'odeur tend à envahir toutes les pièces. Mais plus le gaz se répand, et moins son odeur est sensible car il se dilue dans une quantité d'air de plus en plus grande
=> Le gaz envahit tout l'espace qu'il lui est offert, mais plus l'espace est large, plus la concentration est faible
I MISE EN ÉVIDENCE DES PRESSIONS PARTIELLES
a) Expérience de BERTHOLET
|
Pp H2 = 1 b * 100% = 1 b Pp H2 = 1 b * 50% = 0.5b Pp CO2 = 1 b * 100% = 1 b Pp CO2 = 1 b * 50% = 0.5 b |
Chaque gaz occupant la moitié de chaque réservoir, on peut dire aussi qu'il occupe une partie de la pression dans chaque réservoir. Cette partie de la pression sera appelé pression partielle. Cette expérience justifie que l'on admette que la pression de chaque gaz d'un mélange est proportionnelle à la concentration de chaque gaz dans ce mélange et que la somme de ces pressions est égale à la pression totale. |
Définition de la pression partielle :
La pression partielle d'un gaz dans un mélange est égale à la pression qu'il aurait s'il occupait à lui seul le volume total.
b) Calcul de la pression partielle à partir de Mariotte :
- Dans une cuve de 100 litres on introduit de l'air à 1 bar. Nous avons donc 80 l d'azote et 20 l d'oxygène.
- En utilisant la loi de Mariotte, on calcule la pression de l'oxygène en imaginant qu'on ai retiré tout l'azote. L'oxygène utilise donc tout le volume disponible.
- P1 V1 = P2 V2 => P2 = P1 V1 / V
- => P2 = 1 * 20 / 100
- => P2 = 0.2 bar
- La pression partielle de l'oxygène est de 0.2 bar.
- On effectue la même expérience pour l'azote, celui-ci occupant tout le volume, on obtient :
- P1 V1 = P2 V2 => P2 = P1 V1 / V
- => P2 = 1 * 80 / 100
- => P2 = 0.8 bar
- La pression partielle de l'azote est de 0.8 bar.
- La somme des deux pressions partielles PPO2 + PPN2 = P abs
- 0.2 bar + 0.8 bar = 1 bar
- Quelque soit la pression absolue, on obtiendra toujours : PP=P abs * % et Somme des PP = P abs
II LOI DE DALTON
- Dans un mélange gazeux, chaque gaz se comporte comme s'il était seul à occuper le volume totale occupé par le mélange
- Dans un mélange gazeux, la somme des pressions partielles de chaque gaz est égale à la pression totale exercée sur le mélange
- La pression partielle d'un gaz dans un mélange est égale au produit de la pression totale du mélange par le pourcentage du gaz considéré dans le mélange
Pp = Pa * %
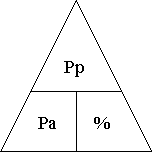
Moyen facile de se rappeler des formules :Pp = Pa * % Pa = Pp / % % = Pp / Pa |
 |
Exemples chiffrés :
- Un mélange gazeux est composé de 50% N2, 40% O2, 10% H2
- Quelles sont les pressions partielles de ces gaz en surface, à 10 m, à 20 m, à 30 m et à 40 m ?
- Surface : Pa = 1 bar
- Pp N2 = Pa * % => Pp N2 = 1 * 50% = 0.5 bar
- Pp O2 = Pa * % => Pp O2 = 1 * 40% = 0.4 bar
- Pp H2 = Pa * % => Pp H2 = 1 * 10% = 0.1 bar
- et Pp N2 + Pp O2 + Pp H2 = 1 b = Pa
- A 10 mètres: Pa = 1 bar
- Pp N2 = Pa * % => Pp N2 = 2 * 50% = 1 bar
- Pp O2 = Pa * % => Pp O2 = 2 * 40% = 0.8 bar
- Pp H2 = Pa * % => Pp H2 = 2 * 10% = 0.2 bar
- et Pp N2 + Pp O2 + Pp H2 = 2 b = Pa
- A 20 mètres: Pa = 3 bar
- Pp N2 = Pa * % => Pp N2 = 3 * 50% = 1.5 bar
- Pp O2 = Pa * % => Pp O2 = 3 * 40% = 1.2 bar
- Pp H2 = Pa * % => Pp H2 = 3 * 10% = 0.3 bar
- et Pp N2 + Pp O2 + Pp H2 = 3 b = Pa
- A 30 mètres: Pa = 4 bar
- Pp N2 = Pa * % => Pp N2 = 4 * 50% = 2 bar
- Pp O2 = Pa * % => Pp O2 = 4 * 40% = 1.6 bar
- Pp H2 = Pa * % => Pp H2 = 4 * 10% = 0.4 bar
- et Pp N2 + Pp O2 + Pp H2 = 4 b = Pa
- A40 mètres: Pa = 5 bar
- Pp N2 = Pa * % => Pp N2 = 5 * 50% = 2.5 bar
- Pp O2 = Pa * % => Pp O2 = 5 * 40% = 2 bar
- Pp H2 = Pa * % => Pp H2 = 5 * 10% = 0.5 bar
- et Pp N2 + Pp O2 + Pp H2 = 5 b = Pa
Chaque fois, la somme des Pressions Partielles est égale à la Pression Absolue
III APPLICATIONS A LA PLONGÉE
| - Calcul des tables de plongée | |
| - Accidents dus à la toxicité des gaz | |
| - Les plongées au mélange | |
| - L'oxygénothérapie hyperbare |
- Exercices :
- Air 80% N2 et 20% O2
- Pp O2 et Pp N2 à 40 mètres ?
- Pp O2 = 5 * 20% = 1 b
- Pp N2 = 5 * 80% = 4 b ==> Pp O2 + Pp N2 = 5 b
A quelle profondeur a t on Pp O2 = 1.7 b ?
- Pa = Pp / % ==> Pa = 1.7 / 0.20 = 8.5 b
- La profondeur est de 75 mètres
Pour quelle proportion O2 N2 a t on Pp O2 = 1.7 b à 40 mètres ?
- % = Pp / Pa ==> % = 1.7 / 5 = 0.34
- Le pourcentage de O2 = 34% et N2 = 66%
Quelle est la Pp N2 contenu dans l'air respiré à 20 mètres ?
Pp = Pa * % ==> Pp = 3 * 0.80 = 2.4 b
A quelle profondeur se trouve un plongeur qui respire de l'air dont la Pp O2 = 0.5 b
- Pa = Pp / % ==> Pa = 0.5 / 0.20 = 2.5 b
- La profondeur est de 15 mètres
- Avec 40% O2 et 60% N2 à 40 mètres
- A quelle profondeur aurait-on la même Pp N2 avec de l'air ?
Pp à 40 m : PP = Pa * % ==> Pp = 5 * 0.60 = 3 b
On recherche la Pa à laquelle Pp N2 = 3 b avec de l'air
- Pa = Pp / % ==> Pa = 3 / 0.80 = 3.75 b
- La profondeur est de 27.5 mètres
Quel mélange O2/N2 doit-on confectionner pour avoir à 30 m la PpN2 de l'air à 15 m
- Pp N2 de l'air à 15 ml : Pp = Pa * % ==> Pp = 2.5 * 0.8 = 2 b
- Pourcentage pour qu'à 30 m on ait la même Pp N2 :
- % = Pp / Pa ==> % = 2 / 4 = 0.5
- Le mélange doit être composé de 50% O2 et de 50% N2
